The Complex numbers in real life

In this article, I will show the utility of complex numbers, and how physicists describe physical phenomena using this kind of number.

What is the complex number?

A complex number can be written in this form:

$$ z=x+iy $$

Where x and y is the real number, and

$$ i=\sqrt{-1} $$

In complex numbers, x is called the real part and y is called the imaginary part.

For example:

$$ z=3+5i $$

$$ z=6+4i $$

The imaginary part is not something that doesn’t exist, but it is only the part of the complex number.

Real Numbers:

Real numbers are all positive and negative integers numbers (…,-3, -2, -1, 0, 1, 2, 3, 4, …), rational numbers that can be written in the fraction or ratio (e.g. 1/2 or 0.5) and irrational numbers that can’t be written in the fraction or ratio because it has infinite numbers after the decimal point.
e.g.

$$ \sqrt2=1.41421356237\ldots\ $$

$$ \pi=3.14159265359\ldots $$

Dimensions:

Dimension is the way to describe the point (position or direction of motion) by writing it down.

If you are familiar with playing chess and use chess notation to write down all moves in chess, you can understand the dimensions in a very easy way. But don’t worry, I will explain it in detail.

In chess, you can notice some numbers and letters on the corner of the chessboard. I can describe any position of a chess piece by using these numbers and letters.

For example, if I want to describe the position of the left knight, I can write “b1”. And if I want to describe the motion of this knight, I can write the final position “c3”.

In this very basic example, you can consider these numbers and letters as coordinates (two-dimensional coordinates). In addition, you use these coordinates to describe the position of any chess pieces.

But What Does N Dimensions Mean?

While you read a book, you will notice some topics deal with 4 dimensions or even 12 dimensions. But as we know, the real world is three dimensions only.

One dimension can describe any point (or thing) on a straight line (e.g. street).

Two dimensions can describe any point on the plane (e.g. GPS on your phone)

Three dimensions can describe any point in space.

From our understanding, the dimension is the way to write down the position of any point or object.

If you want to describe the position of a point in space, you need three dimensions. But if the point moves over time, you will need to add one more dimension that contains time. In this case, we have four dimensions.

Ok, what about the five dimensions?

In complex motion like the CNC machine, you need to give the machine-specific information about the position that works in.

The arm of CNC may have many motors (motor units) and each motor can move in three dimensions.

If you have two motors can each one move in three dimensions, you have now six dimensions. And you must write down the six dimensions in the program software of that machine.

In this picture, this CNC arm has a motor moving in one dimension (1D) (up and down) and the other two motors move in two dimensions (2D)(up and down, and rotate). Therefore, this is five dimensions (5D) CNC arm.

Phase difference:

If you want to make an experiment and try to count how many rotations of your fan per minute. Of course, you should have a very slow fan to make this experiment easy for you.

While you count the rotation, you need a fixed point (like something in your room). Every time the fan blade reaches this fixed point, you increase the count.

If you begin this experiment and the fan blade is not at the fixed point, the distance (rotational angle) between the fixed point and the fan blade is the phase difference.

Any delay between two physical phenomena can describe as a phase difference.

For example, if you apply AC voltage to the conductor coil, the current across this coil will be delayed with respect to voltage. In this case, we have a phase difference between voltage and current.

The importance of complex numbers in real life:

In real numbers, we can represent this number as a straight line.

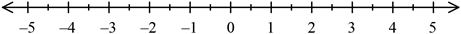
A real number can store information about the value of the number and if this number is positive or negative.

But in the complex number, we can represent this number (z = a + ib) as a plane.

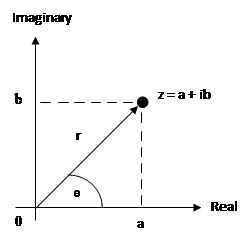
If you notice, this number has one more piece of information. This new information is the angle (θ).  

To extract this information from the complex number

$$ z=a+ib $$

by using these relations.

$$ r=\sqrt{a^2+b^2} $$

$$ \theta=\tan^{-1}{\left(\frac{b}{a}\right)} $$

Where

 r is the absolute value of the complex number, or the distance between the origin point (0,0) and (a,b) point.

In this example, z = 2 + 3i

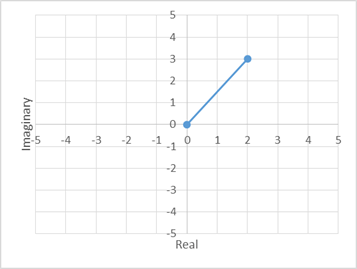
$$ r=\sqrt{2^2+3^2} $$

$$ \theta=\tan^{-1}{\left(\frac{3}{2}\right)} $$

In most cases, this angle (θ) is used as a phase difference.

From trigonometry and right-angled triangle:

$$\sin{\theta=\frac{Opposite}{Hypotenuse}}$$

$$\cos{\theta=\frac{Adjacent}{Hypotenuse}}$$

$$ \tan{\theta}=\frac{Opposite}{Adjacent} $$

From these

$$ \cos{\theta=\frac{a}{r}} $$

$$ a=r\cos{\theta} $$

$$ \sin{\theta=\frac{b}{r}} $$

$$ b=r\sin{\theta} $$

$$ z=a+ib $$

$$ z=r\cos{\theta+i\ (r\sin{\theta)}\ } $$

$$ z=r\left(\cos{\theta+i\sin{\theta}}\right) $$

From Euler’s formula:

$$ e^{i\theta}=\cos{\theta+i\sin{\theta}} $$

$$ z=r\ e^{i\theta} $$

There are many applications that use complex numbers instead of real numbers to represent the value of physical phenomena in real life because of the importance to store the phase shift inside these numbers.

The equation of wave and the phase angle:

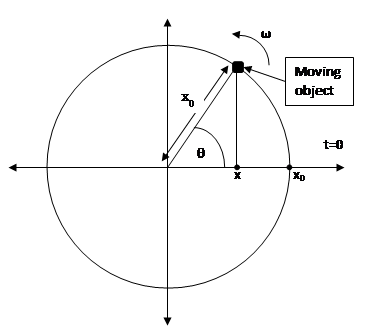
If an object moves in a uniform circle, the equation of the projection of this object in the x-axis is

$$ x=x_0\cos{\theta} $$

And the angle velocity (ω) is equal to

$$ \omega=\frac{\theta}{t} $$

Where t is the time and x₀ is the amplitude (the largest displacement from equilibrium)

$$ \theta=\omega t $$

$$ x=x_0\cos{\left(\omega t\right)} $$

But if we choose t=0 anywhere else.

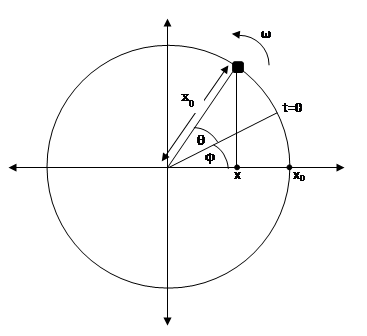
$$ x=x_0\cos{\left(\theta+\phi\right)} $$

Where φ is the phase angle.

$$ x=x_0\cos{\left(\omega t+\phi\right)} $$

The importance of complex numbers in travelling waves

In the travelling wave, the complex number can be used to simplify the calculations by converting trigonometric functions (sin(x) and cos(x)) to exponential functions (ex) and storing the phase angle into a complex amplitude.

The angle velocity (ω) unit is radians per second. If you measure an angle in radians, you can simply calculate the length of the arc.

The circumference (C) of the circle is

$$ C=2\pi r $$

And the circumference (C) of the unit circle (r=1) is

$$ C=2\pi $$

The angle of the complete circle is (2π) in radians. Therefore, in the unit circle, you can deal with an angle in radians as the length of the arc.

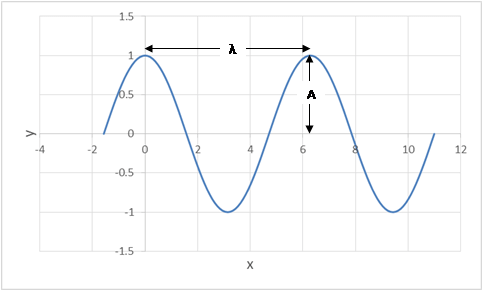
The equation of the non-travelling wave

The equation of the non-travelling wave is

$$ y\left(\theta\right)=A\cos{\theta} $$

$$ \theta=2\pi\frac{x}{\lambda} $$

Because (2π) is the angle of full-wave

In the full-wave:

$$ x=\lambda $$

$$ \theta=2\pi\left(\frac{\lambda}{\lambda}\right)=2\pi $$

And in the half-wave:

$$ x=\frac{\lambda}{2}=\left(\frac{1}{2}\right)\lambda $$

$$ \theta=2\pi\frac{x}{\lambda} $$

$$ =2\pi\left(\left(\frac{1}{2}\right)\frac{\lambda}{\lambda}\right) $$

$$ =2\pi\left(\frac{1}{2}\right)=\pi $$

For the quarter-wave:

$$ x=\frac{1}{4}\lambda $$

$$ \theta=2\pi\frac{x}{\lambda} $$

$$ =2\pi\left(\left(\frac{1}{4}\right)\frac{\lambda}{\lambda}\right) $$

$$ =2\pi\left(\frac{1}{4}\right)=\frac{\pi}{2} $$

From that

$$ \theta=2\pi\frac{x}{\lambda} $$

Then

$$ y\left(x\right)=A\cos{\left(2\pi\frac{x}{\lambda}\right)} $$

The equation of the travelling wave

If you want to make any wave travel with velocity (v), you should replace any x with (x – vt) if the motion is in the positive direction, and (x + vt) if the motion is in the negative direction.

But why.

Consider a point (x) move in a line.

This point (x) moves from x₁ to x₂ with velocity (v) in (t) time.

$$ v=\frac{Distance}{Time}=\frac{x_2-x_1}{t} $$

$$ vt=x_2-x_1 $$

$$ x_1=x_2-vt $$

Any positive change of (x) will subtract with the same amount of change (vt). Therefore, we can convert any wave to a travelling wave by replacing (x) with (x-vt) in the positive and (x+vt) in the negative direction.

Then, the travelling wave equation is

$$ y\left(x,t\right)=A\cos{\left(\frac{2\pi}{\lambda}\left(x-vt\right)\right)} $$

We can use the wavenumber k to simplify this equation, where the number is 

$$ k=\frac{2\pi}{\lambda} $$

And

$$ v=\frac{\lambda}{T} $$

Where v is the velocity of the travelling wave.

$$ \frac{1}{T}=\frac{v}{\lambda} $$

And T is the periodic time.

And also

$$ \omega=\frac{2\pi}{T} $$

Substitute in equation

$$ \omega=2\pi\frac{v}{\lambda}=\frac{2\pi}{\lambda}v=kv $$

$$ v=\frac{\omega}{k} $$

Then, the equation of the travelling wave is

$$ y\left(x,t\right)=A\cos{\left(k\left(x-\frac{\omega}{k}t\right)\right)} $$

$$ y\left(x,t\right)=A\cos{\left(kx-\omega t\right)} $$

If you have the phase difference angle (φ)

$$ y\left(x,t\right)=A\cos{\left(kx-\omega t+\phi\right)} $$

We can simply this equation by converting it from trigonometric functions (sin(x) and cos(x)) to exponential functions (e^x) using complex wave function.

$$ y\left(x,t\right)=A\ e^{i\left(kx-\omega t+\phi\right)} $$

But this equation equal to

$$ y\left(x,t\right)=A\cos{\left(kx-\omega t+\phi\right)+i\ A\sin{\left(kx-\omega t+\phi\right)}} $$

We will neglect the imaginary part and deal with the real part only. This is because we want to simplify the original equation for calculations.

Now we want to store the phase difference angle inside the complex amplitude.

The real amplitude (A) should be converted to a complex amplitude (y₀).

$$ y\left(x,t\right)=Ae^{i\left(kx-\omega t\right)}e^{i\phi} $$

$$ y\left(x,t\right)=\left(Ae^{i\phi}\right)e^{i\left(kx-\omega t\right)} $$

The complex amplitude (y₀) is

$$ y_0=Ae^{i\phi} $$

From that, the complex form of the one-dimensional travelling wave equation is

$$ y\left(x,t\right)=y_0e^{i\left(kx-\omega t\right)} $$

In this equation, we used the complex function to simplify the calculations and used the complex amplitude to store the phase difference angle.

Conclusion

In real numbers you can store the information of magnitude (scale value) for example “5” and if that value is positive or negative. But in complex numbers, you can store one more piece of information “angle”, and this angle in most cases used as a phase difference angle.

The complex numbers can be used also to simplify the calculations by converting trigonometric functions (sin(x) and cos(x)) in equations to exponential functions (ex) by adding an imaginary part to these equations and using Euler’s formula:

$$ e^{i\theta}=\cos{\theta+i\sin{\theta}} $$

I hope this article will help you to understand the importance of complex numbers to describe physical phenomena.